7.3 Plotting One Dimension

The simplest plots involve plotting a single vector of numbers, or several such vectors (e.g. for different samples). Each value in the vector typically corresponds to a category or fixed value, for example the tau column from the example above has pairs of (ID, tau value). The order of these numbers can be changed, but the vector remains one dimensional or 1-D.

7.3.1 Bar chart

Bar charts map length (i.e. the height or width of a box) to the scalar value of a number. The difference in visual length can help the viewer notice consistent patterns in groups of bars, depending on how they are arranged:

ggplot(ad_metadata, mapping = aes(x=ID,y=tau)) +
  geom_bar(stat="identity")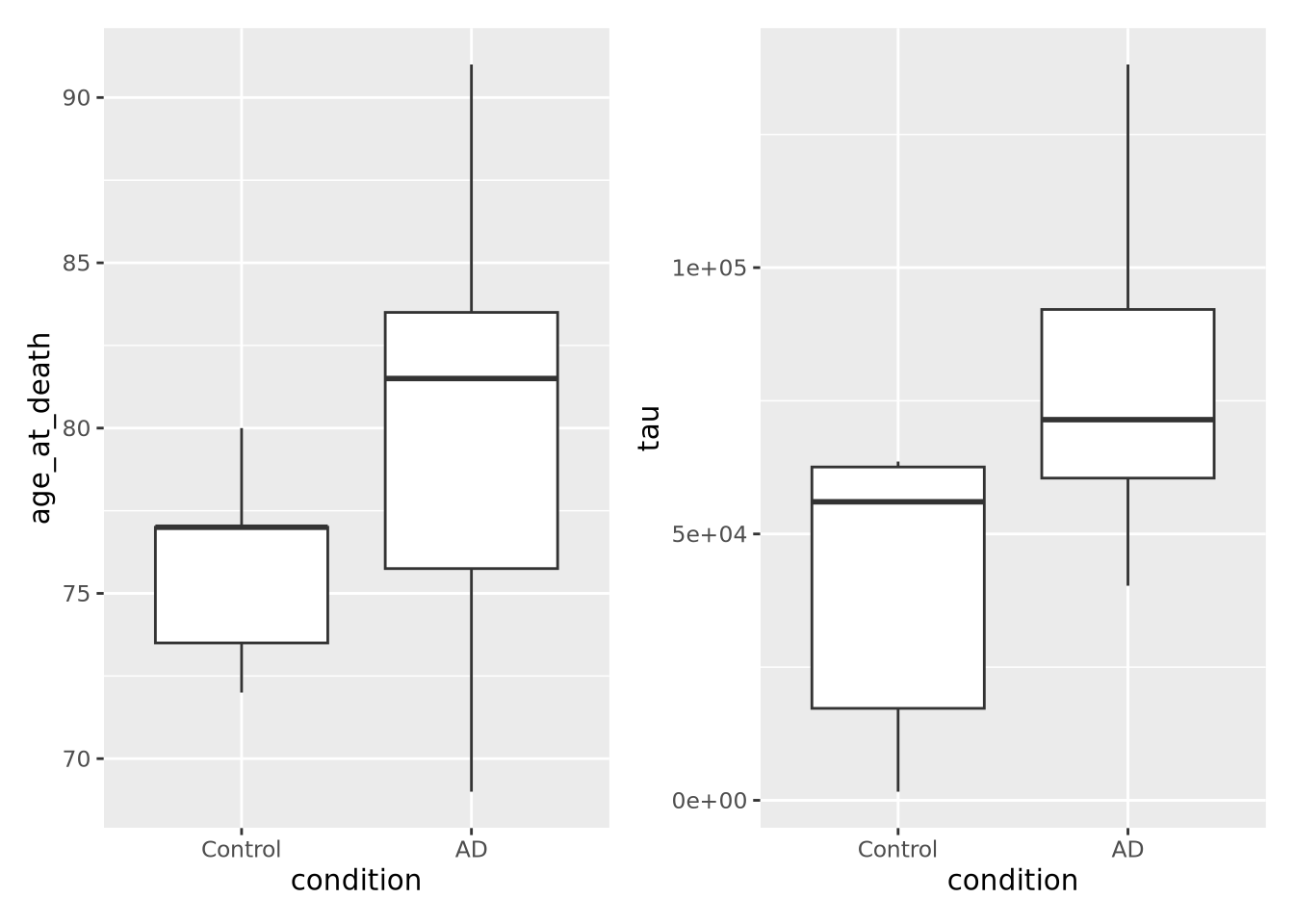

Note the stat="identity" argument is required because by default geom_bar counts the number of values for each value of x, which in our case is only ever one. This plot is not particularly helpful, so let’s change the fill color of the bars based on condition:

ggplot(ad_metadata, mapping = aes(x=ID,y=tau,fill=condition)) +
  geom_bar(stat="identity")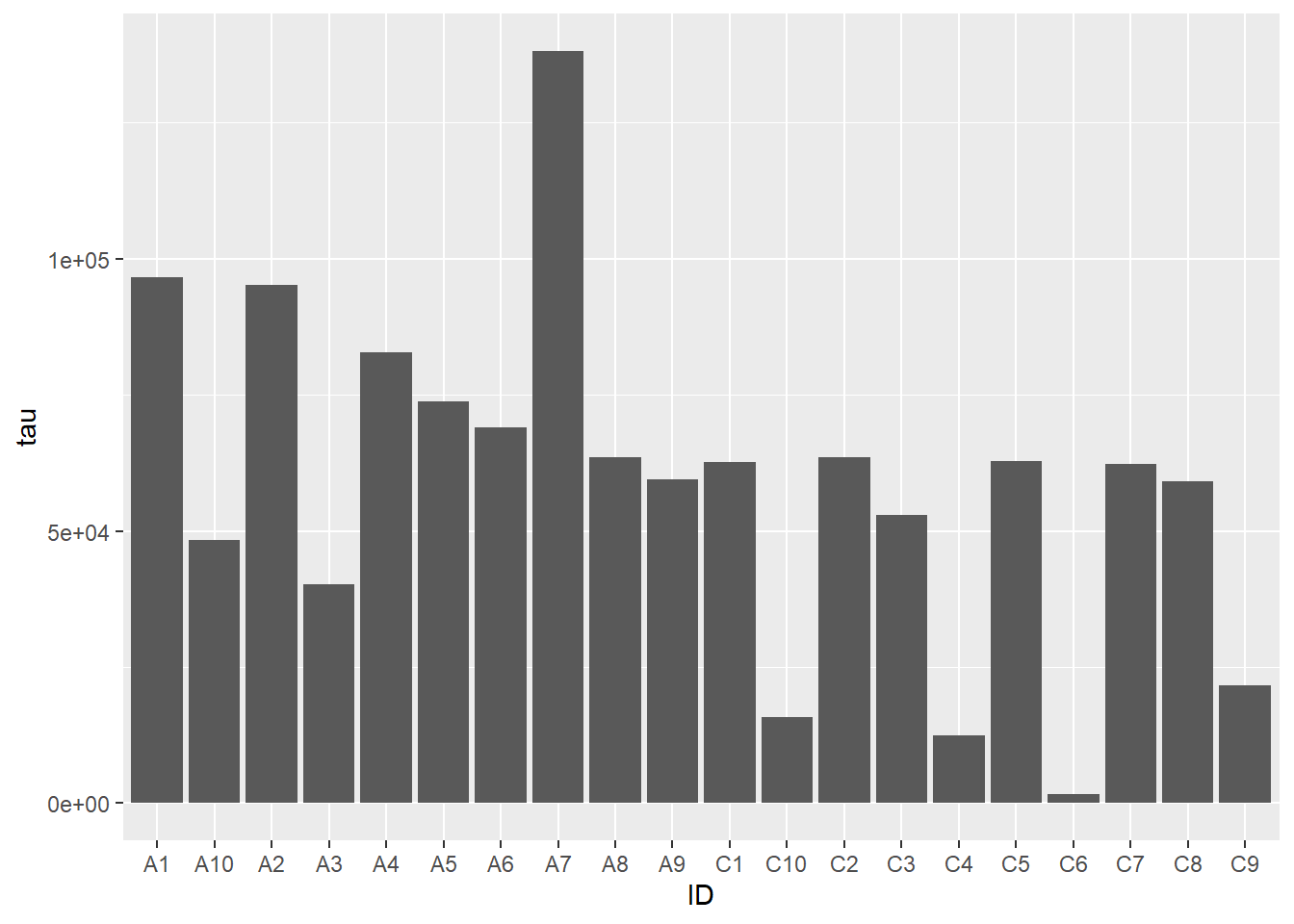

Slightly better, but maybe we can see even more clearly if we sort our tibble by tau first. Sorting elements in these 1-D charts is somewhat complicated, and is explained in the [Reordering 1-D Data Elements] section below.

Bar charts can also plot negative numbers. In the following example, we center the tau measurements by subtracting the mean from each value before plotting:

mutate(ad_metadata, tau_centered=(tau - mean(tau))) %>%
  ggplot(mapping = aes(x=ID, y=tau_centered, fill=condition)) +
  geom_bar(stat="identity")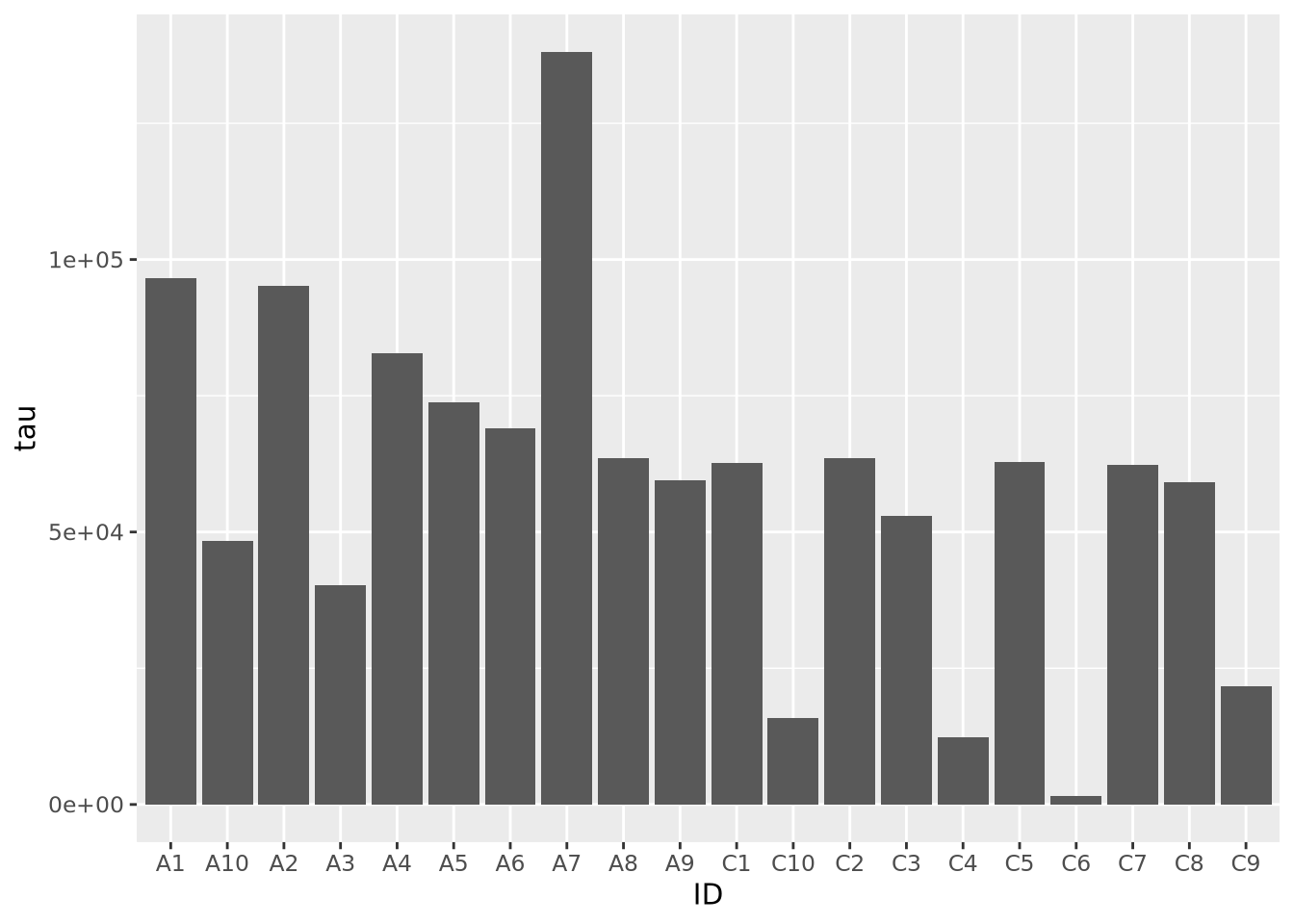

7.3.2 Lollipop plots

Similar to bar charts, so-called “lollipop plots” replace the bar with a line segment and a circle. The length of the line segment is proportional to the magnitude of the number, and the point marks the length of the segment as a height on the y or length on the x axis, depending on orientation.

ggplot(ad_metadata) +
  geom_point(mapping=aes(x=ID, y=tau)) +
  geom_segment(mapping=aes(x=ID, xend=ID, y=0, yend=tau))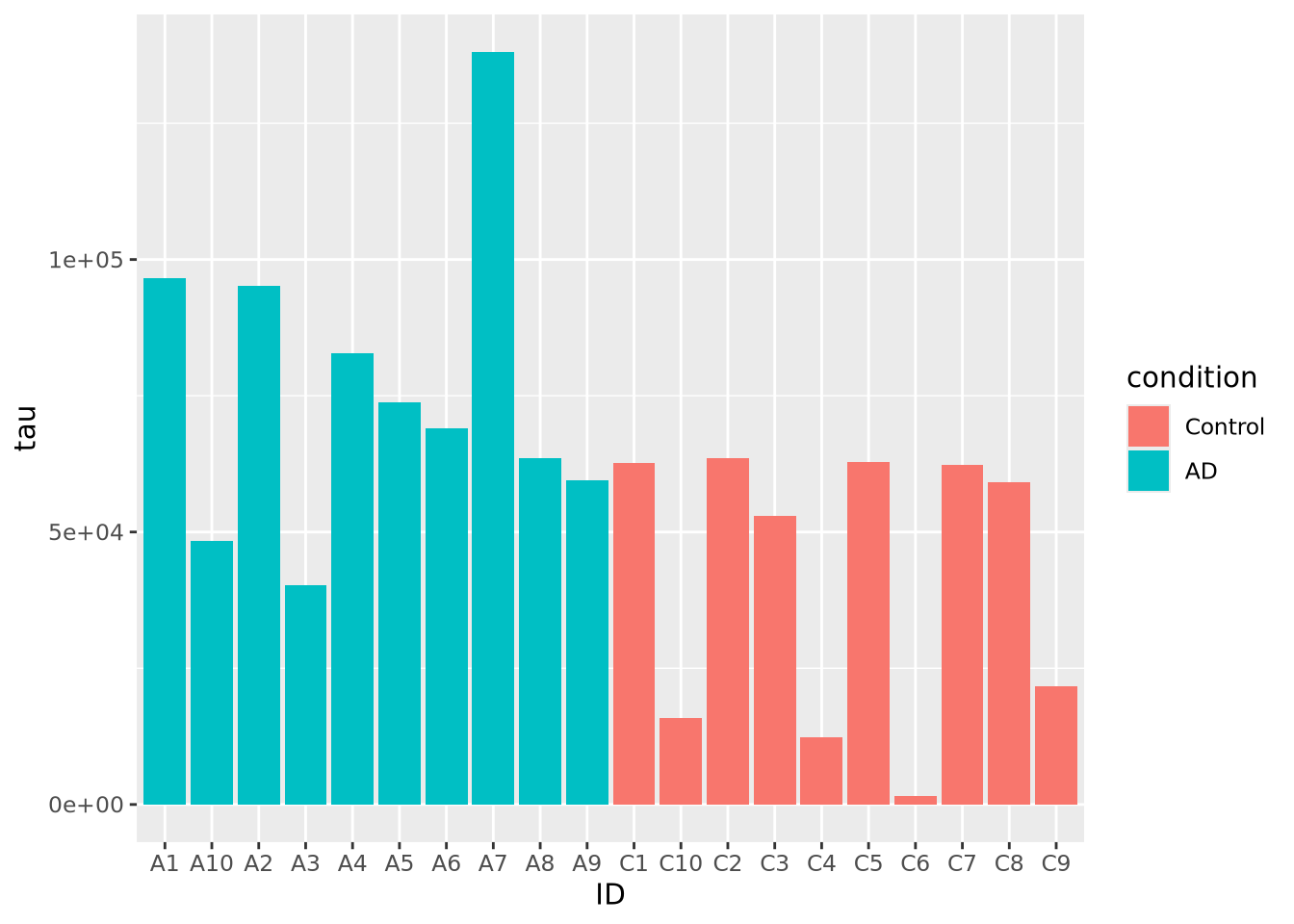

Note that aes() mappings can be made on the ggplot() object or on each individual geometry function call, to specify different mappings based on geometry.

7.3.3 Stacked Area charts

Stacked area charts can visualize multiple 1D data that share a common categorical axis. The charts consist of one line per variable with vertices that correspond to x and y values similar to a bar or lollipop plots. Each variable is plotted using the previous one as a baseline, so that the height of the data points for each category is proportional to their sum. The space between the lines for each variable and the previous one are filled with a color. The following plot visualizes the amount of marker stain for each of the four genes for each individaul:

pivot_longer(
  ad_metadata,
  c(tau,abeta,iba1,gfap),
  names_to='Marker',
  values_to='Intensity'
  ) %>%
  ggplot(aes(x=ID,y=Intensity,group=Marker,fill=Marker)) +
    geom_area()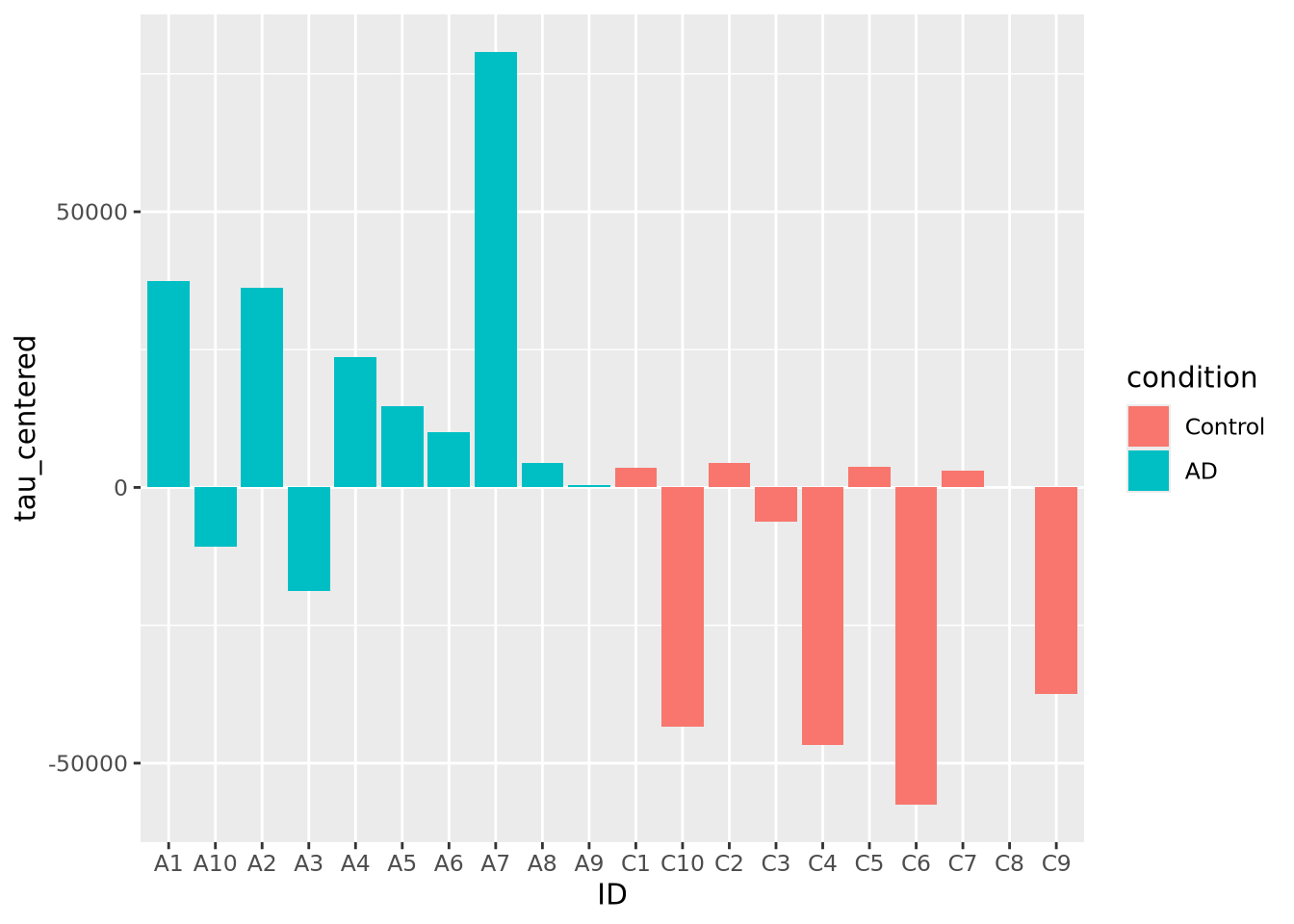

We notice that subject A4 has the highest overall level of marker intensity, followed by A1, A7, etc. The control samples overall have less intensity across all markers. Certain samples, A2 and C5, have little to no abeta aggregation, and C6 has little to no tau.

Stacked area plots require three pieces of data:

x - a numeric or categorical axis for vertical alignment
y - a numeric axis to draw vertical proportions
group - a categorical variable that indicates which (x,y) pairs correspond to the same line

In the example above, we needed to pivot our tibble so that the different markers and their values were placed into columns Marker and Intensity, respectively. Data for stacked bar charts will usually need to be in this ‘long’ format, as described in Rearranging Data.

Sometimes it is more helpful to view the relative proportion of values in each category rather than the actual values. The result is called a proportional stacked area plots. While not a distinct plot type, we can create one by preprocessing our data by dividing each value by the column sum:

pivot_longer(
  ad_metadata,
  c(tau,abeta,iba1,gfap),
  names_to='Marker',
  values_to='Intensity'
  ) %>%
  group_by(ID) %>% # we want to divide each subjects intensity values by the sum of all four markers
  mutate(
    `Relative Intensity`=Intensity/sum(Intensity)
  ) %>%
  ungroup() %>% # ungroup restores the tibble to its original number of rows after the transformation
  ggplot(aes(x=ID,y=`Relative Intensity`,group=Marker,fill=Marker)) +
    geom_area()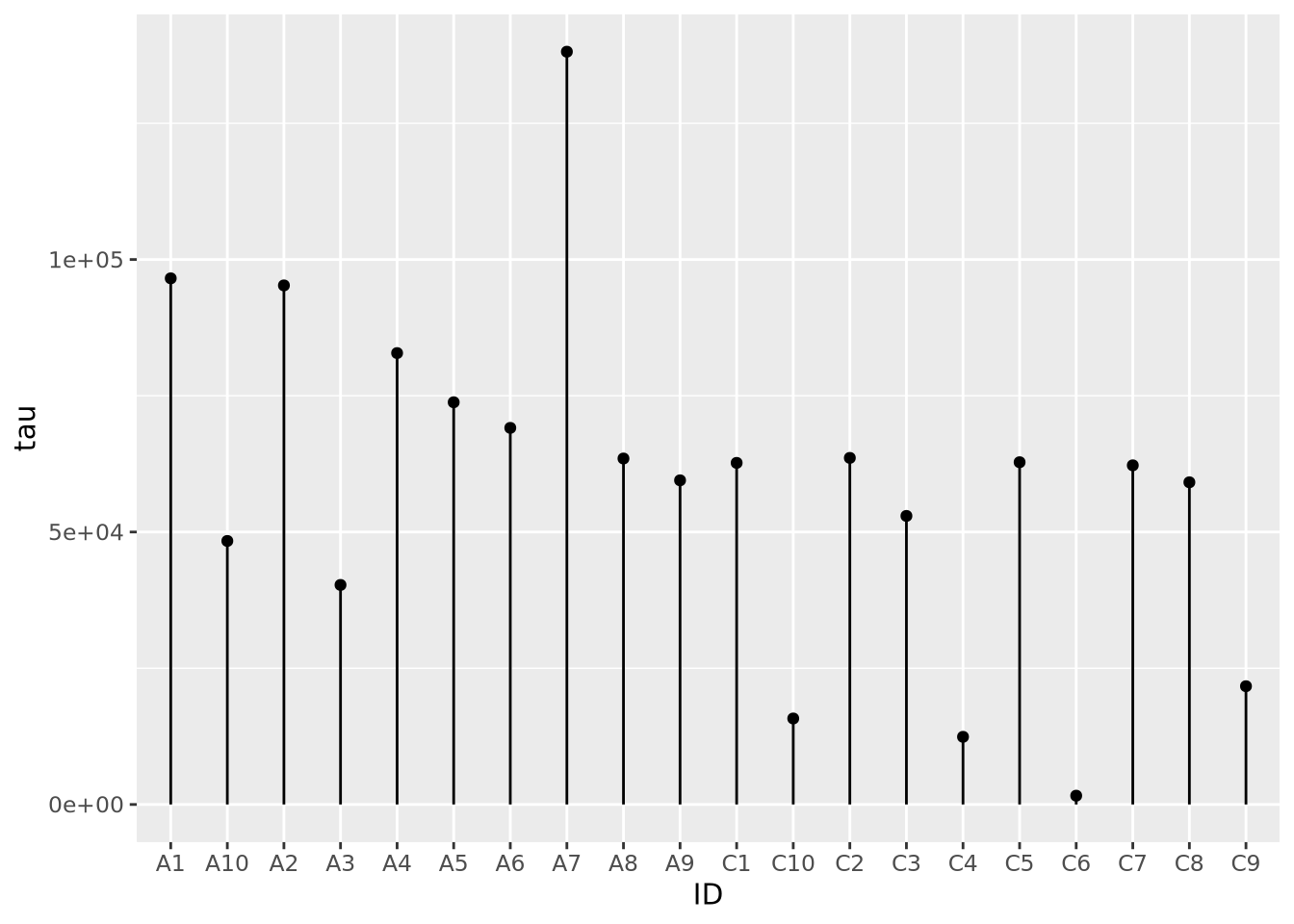

Now the values for each subject have been normalized to each sum to 1. In this way, we might note that the relative proportion of abeta seems to be greater in AD samples than Controls, but that may not be true of tau. These observations may inspire us to ask these questions more rigorously than we have done so far by inspection.