7.6.1 Dendrograms

Dendrograms are visualizations of tree structures (dendron means tree in Greek). In the graph theory branch of mathematics, a tree is defined as a graph composed of nodes and edges in which any two nodes are connected by exactly one path. Such a graph is also called an acyclic graph, where no paths exist that can be followed from a node back to iself. A full treatment of trees and graph theory is beyond the scope of this book, but we will discuss trees to the extent they are necessary to understand how to read a dendrogram.

The concepts of a dendrogram are illustrated in the following figure:

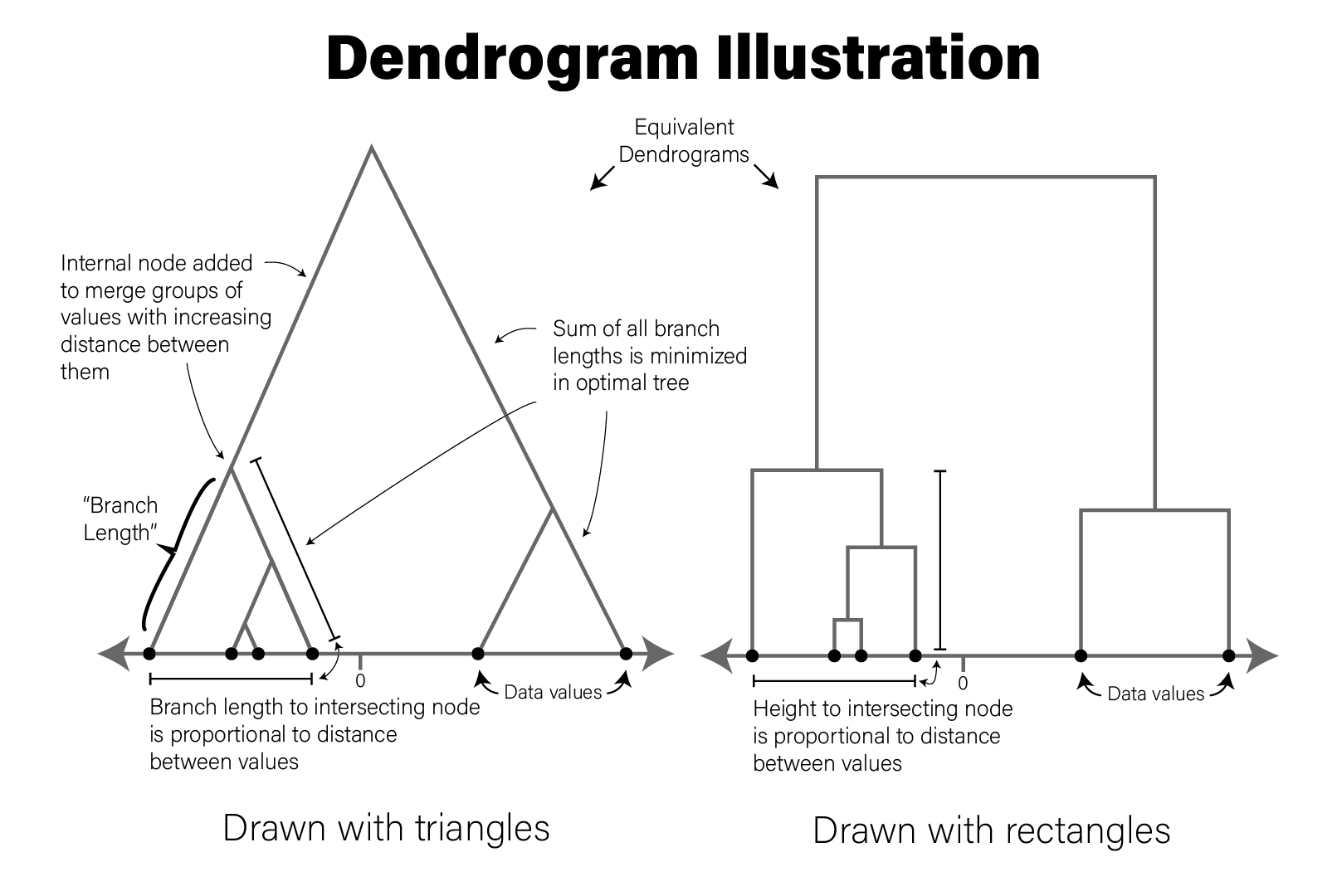
Dendrogram Illustration

The tree drawn in a typical dendrogram is created using the output of a clustering algorithm, e.g. hierarchical clustering that groups data points together based on their dissimilarity. Briefly, in the figure, the data are one dimensional scalars, so the distance between all points is simply the absolute value of the difference between them. The two closest points are then merged into a single group, and the pairwise distances are recomputed for all remaining data points with a summary of this new group (the group summarization method is specified by the user and is called the linkage critera). Then the process repeats, where the two nearest data points or summarized groups are merged into a new group, the new group is summarized, pairwise distances recomputed, etc. until all the data points have been included in a group. In this way, all data points are assigned to a hierarchy of groups. In general, any hierarchical grouping of data can be used to generate a dendrogram.

Given a hierarchical clustering result, a dendrogram can be drawn in several ways in R. Using our AD marker example data, we hierarchically cluster the subjects based on the content of all their markers and visualize the result as follows:

library(ggdendro)

# produce a clustering of the data using the hclust for hierarchical clustering
# and euclidean distance as the distance metric
euc_dist <- dist(dplyr::select(ad_metadata,c(tau,abeta,iba1,gfap)))
hc <- hclust(euc_dist, method="ave")

# add ID as labels to the clustering object
hc$labels <- ad_metadata$ID

ggdendrogram(hc)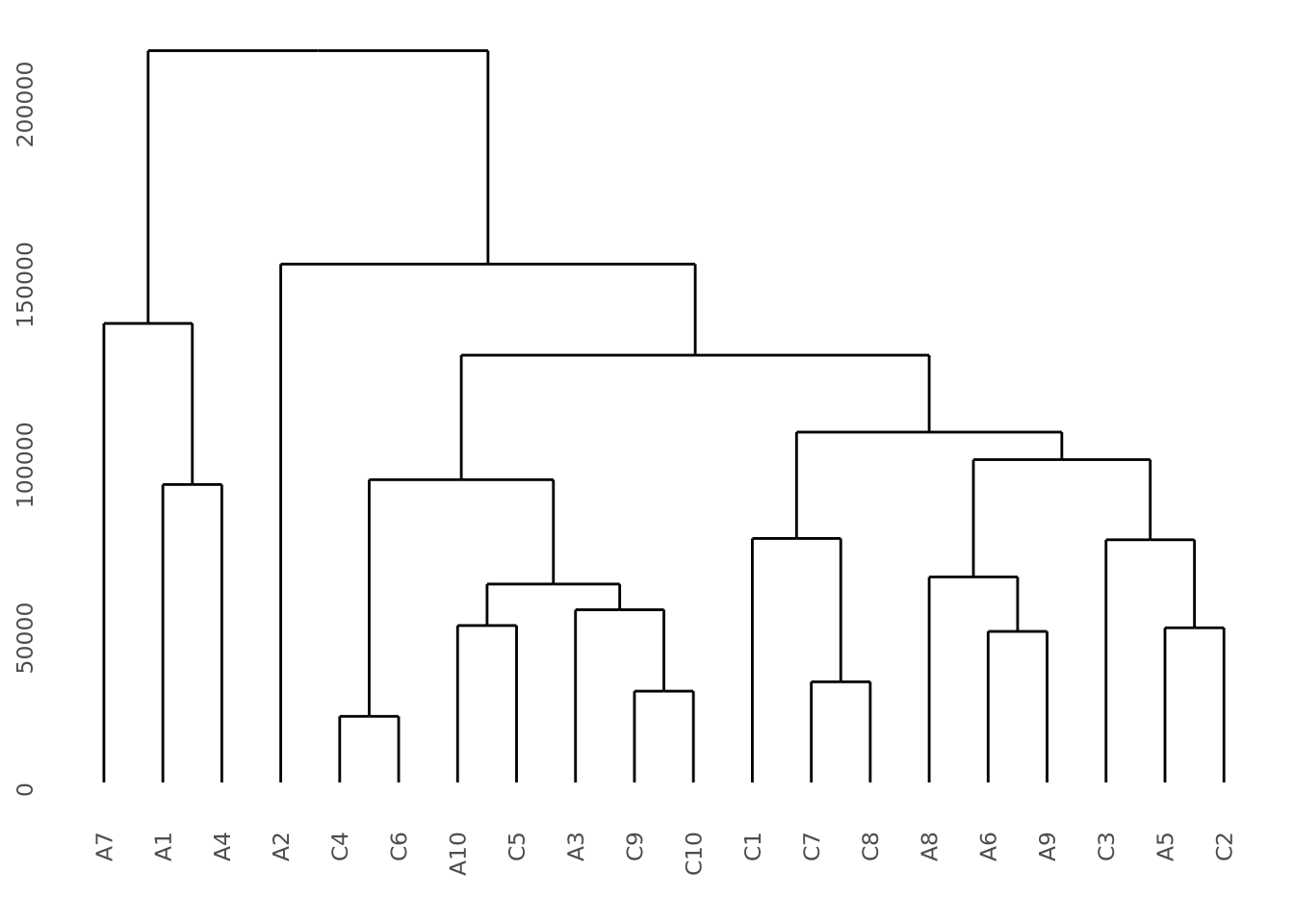

This dendrogram does not produce highly distinct clusters of AD and control samples with all the data.

To illustrate what a dataset with strong clustering looks like, we draw multivariate samples from two normal distributions and cluster the results:

library(patchwork)
library(ggdendro)

well_clustered_data <- tibble(
  ID=c(stringr::str_c("A",1:10),stringr::str_c("B",1:10)),
  f1=c(rnorm(10,0,1),rnorm(10,10,1)),
  f2=c(rnorm(10,0,1),rnorm(10,10,1))
)

scatter_g <- ggplot(well_clustered_data, aes(x=f1,y=f2)) + geom_point()

# produce a clustering of the data using the hclust for hierarchical clustering
# and euclidean distance as the distance metric
euc_dist <- dist(dplyr::select(well_clustered_data,-ID))
hc <- hclust(euc_dist, method="ave")

# add ID as labels to the clustering object
hc$labels <- well_clustered_data$ID

dendro_g <- ggdendrogram(hc)
scatter_g | dendro_g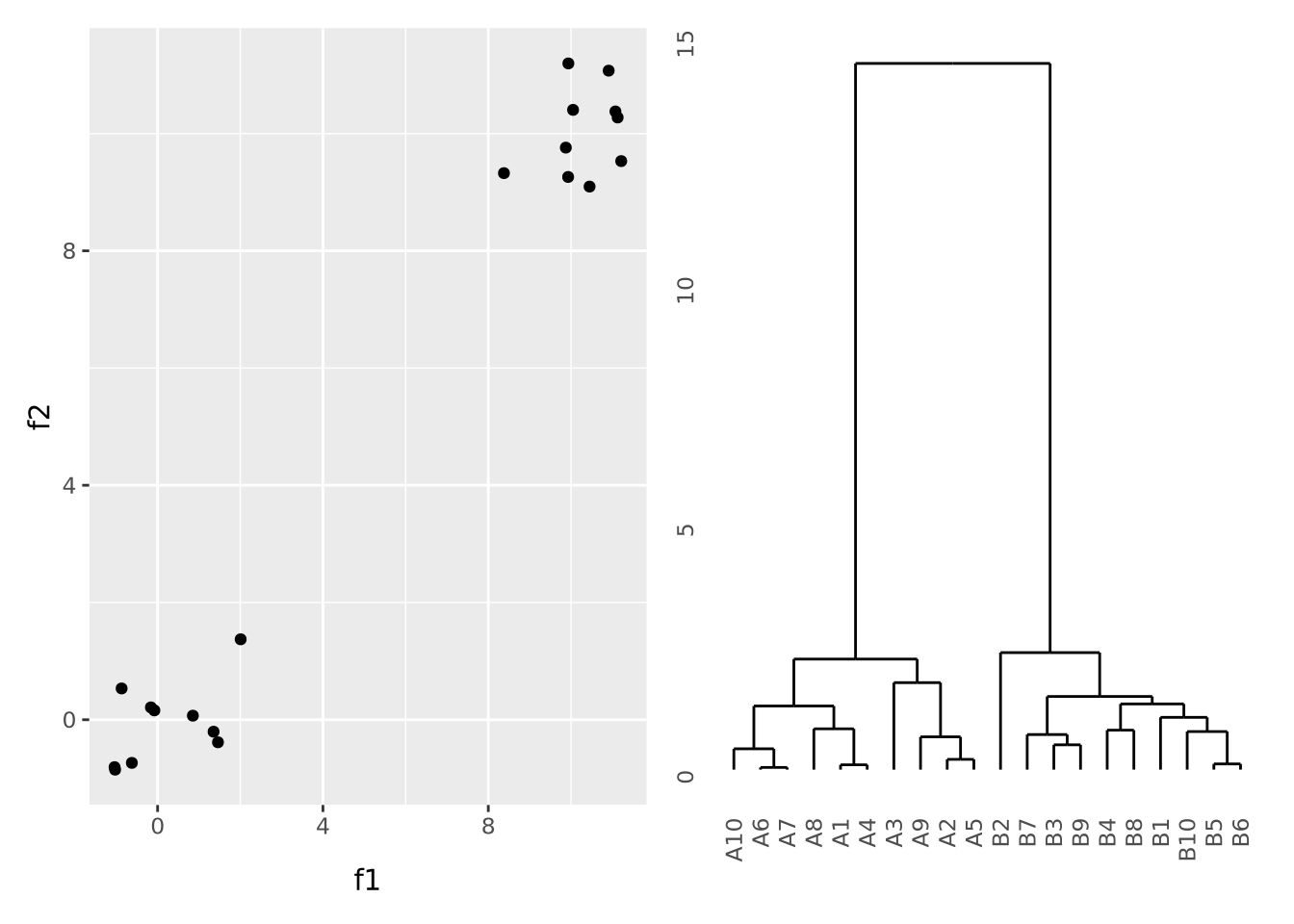

Here, all the A and B samples strongly cluster together, with a large distance between clusters.

7.6.2 Chord Diagrams and Circos Plots

Circos is a software package that creates circular diagrams originally designed to depict genomic features and data. The software is capable of making beautiful, information dense figures. The Circos software itself is written in the Perl programming language, but the circlize package brings these capabilities to R. The following is a basic circos plot created by the circlize package:

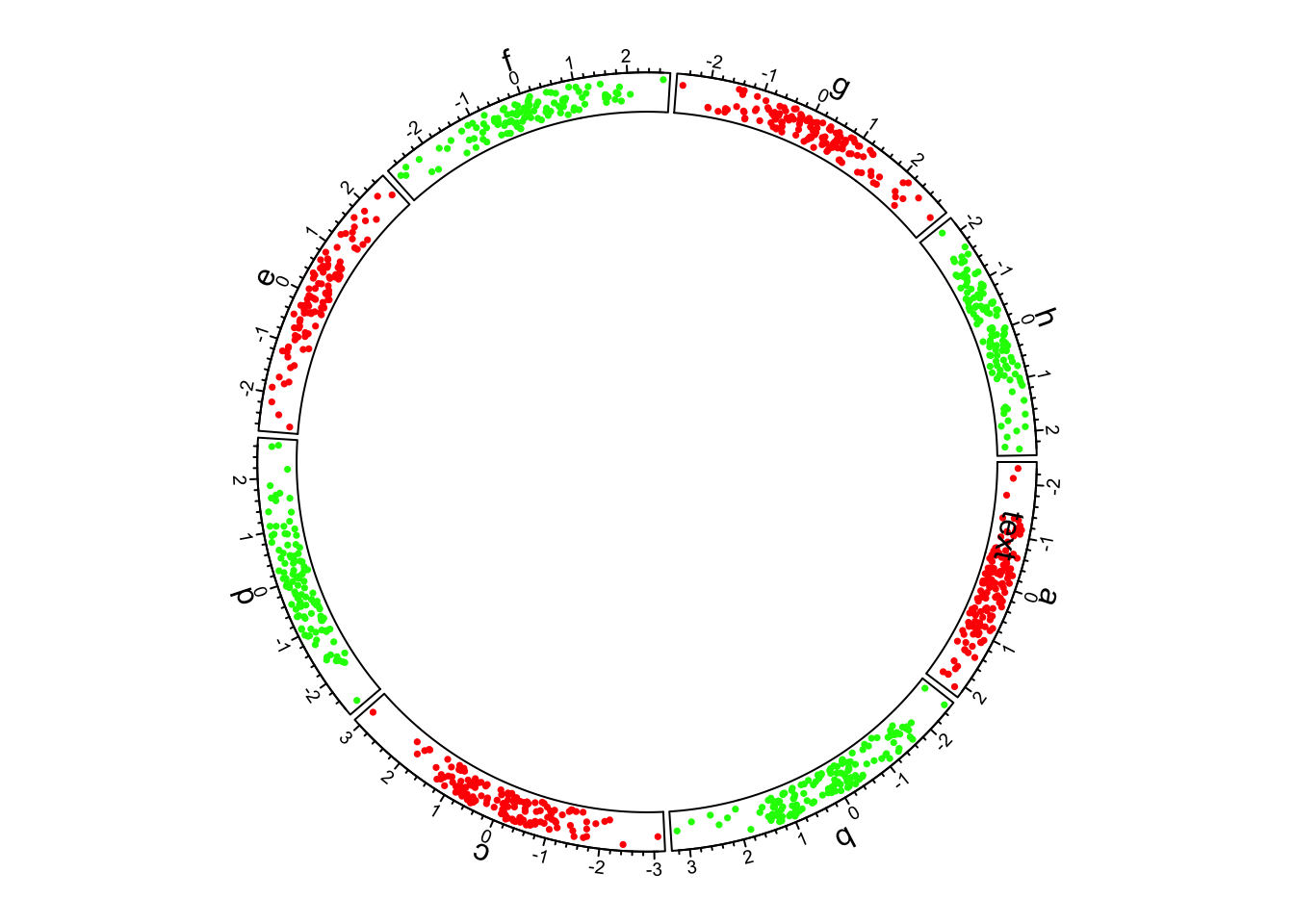
Basic circlize plot

The circle is divided up into 8 sectors here labeled with letters. There is a single track added to the plot, where each sector has a 2-dimensional random dataset plotted within the arc of the sector’s track box. Many tracks may be added to the same plot:

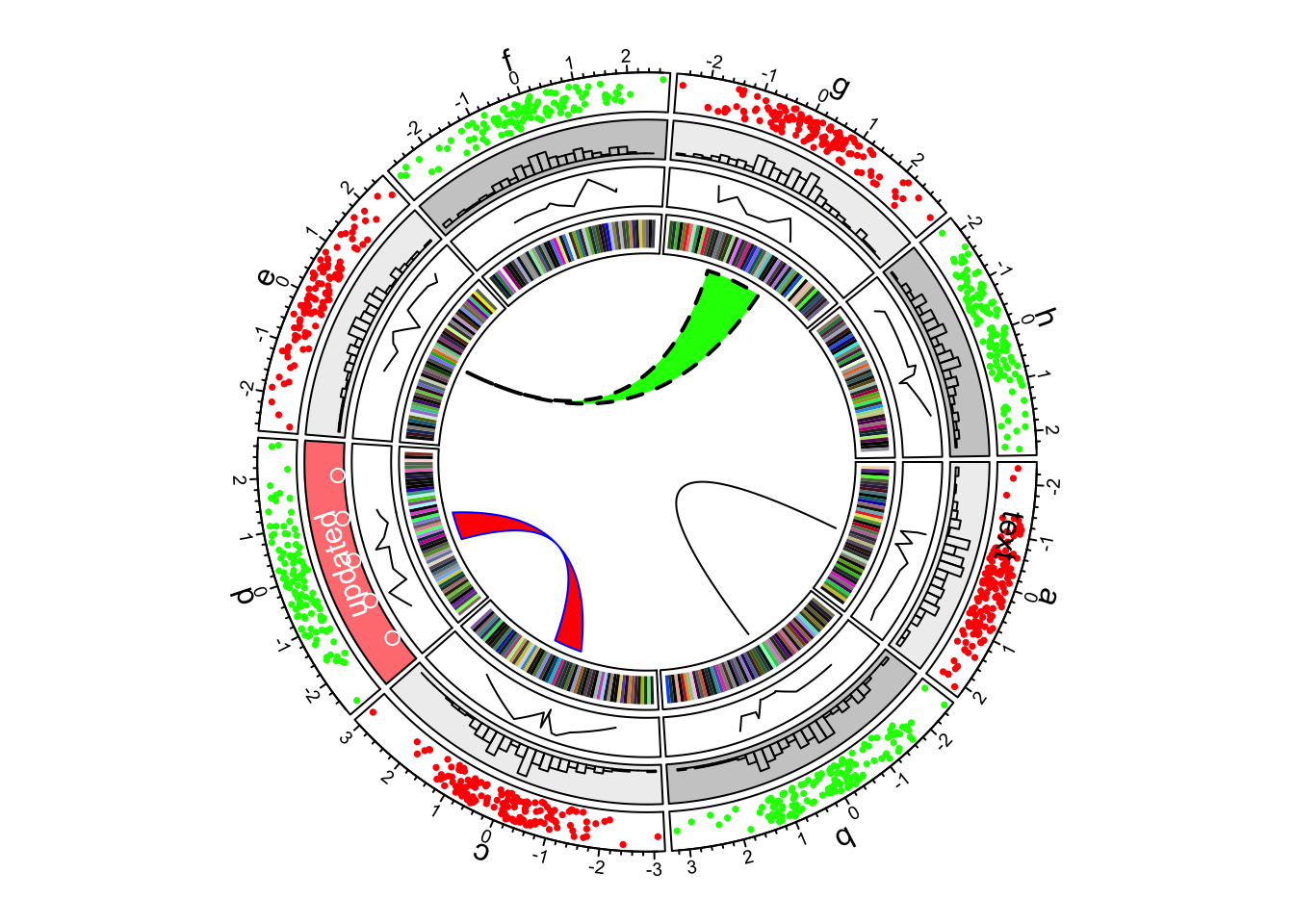
Multiple tracks in a circlize plot

The arches inside the circle are called chords and are drawn to indicate there is a relationship between the coordinates of different sectors. Diagrams with such chords between sectors are called chord diagrams, and some plots are composed only of coords:

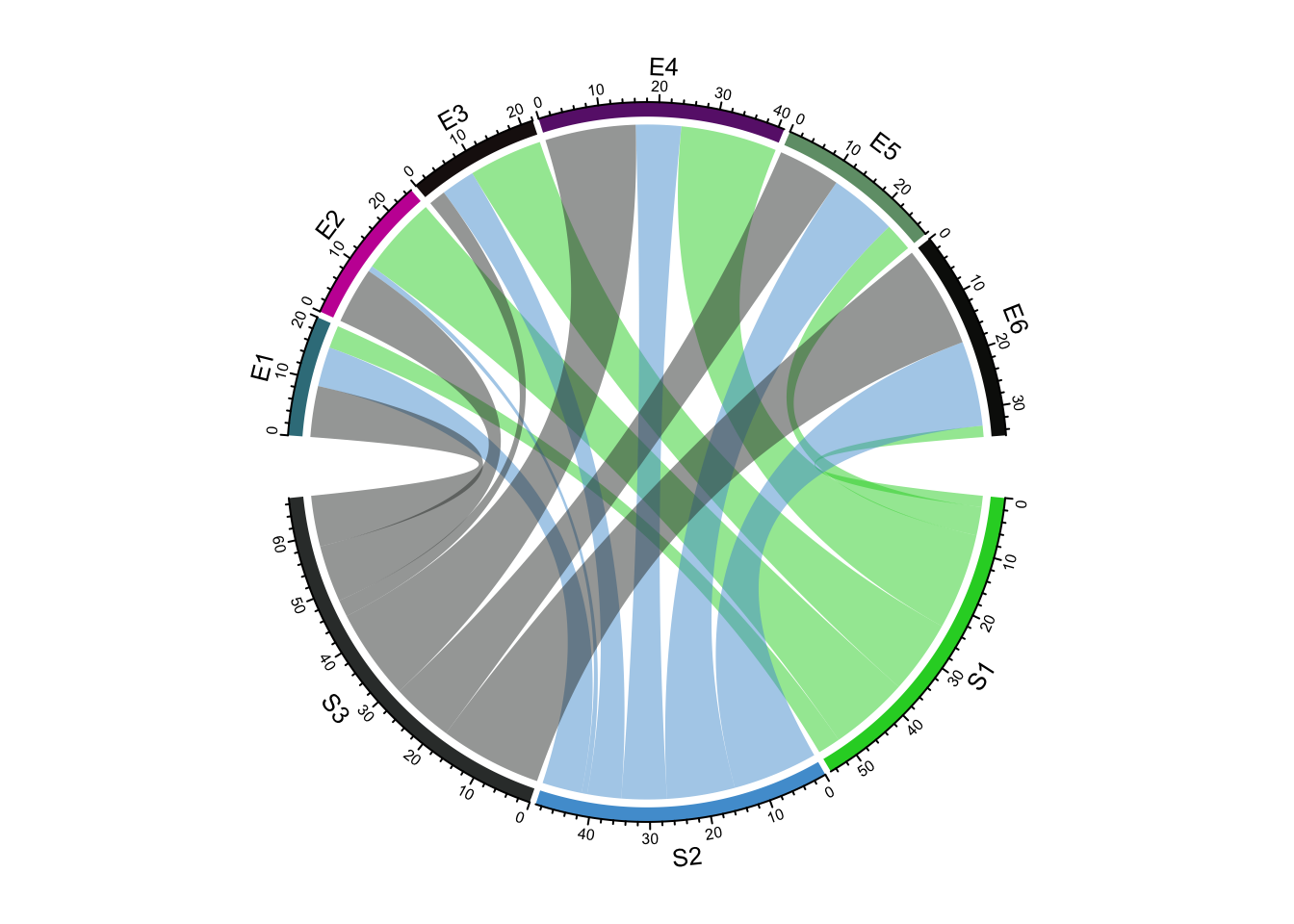
circlize chord diagram

These chord diagrams are often used in genomics studies to illustrate chromosomal rearrangements:

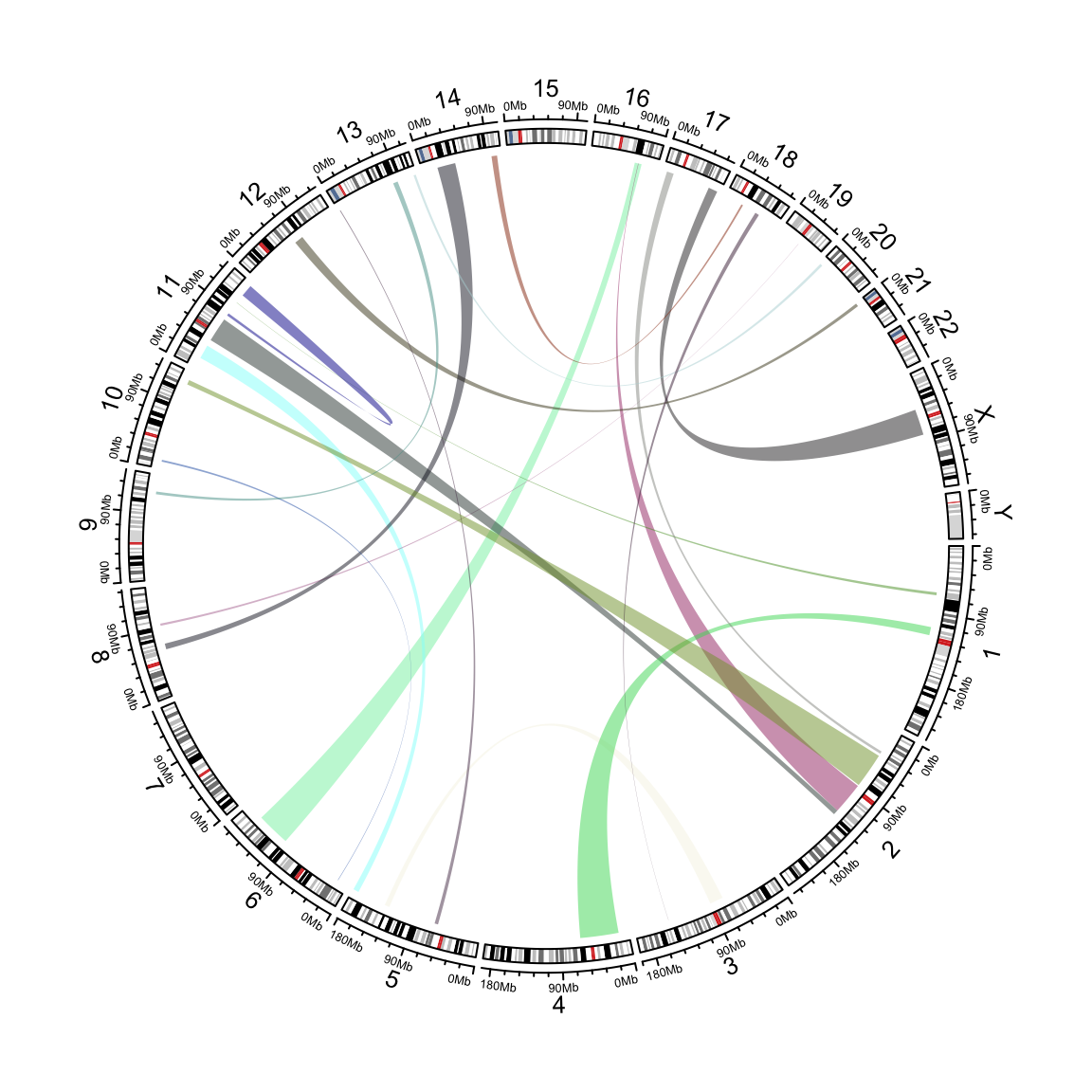
genomic links example

Read the circlize documentation for more information on how to use this very feature rich package.