7.2 Grammar of Graphics

The grammar of graphics is a system of rules that describes how data and graphical aesthetics (e.g. color, size, shape, etc) are combined to form graphics and plots. First popularized in the book The Grammar of Graphics by Leland Wilkinson and co-authors in 1999, this grammar is a major contribution to the structural theory of statistical graphics. In 2005, Hadley Wickam wrote an implementation of the grammar of graphics in R called ggplot2 (gg stands for grammar of graphics).

Under the grammar of graphics, every plot is the combination of three types of information: data, geometry, and aesthetics. Data is the data we wish to plot. Geometry is the type of geometry we wish to use to depict the data (e.g. circles, squares, lines, etc). Aesthetics connect the data to the geometry and defines how the data controls the way the selected geometry looks.

A simple example will help to explain. Consider the following made up sample metadata tibble for a study of subjects who died with Alzheimer’s Disease (AD) and neuropathologically normal controls:

ad_metadata

## # A tibble: 20 x 8
##    ID    age_at_death condition    tau  abeta   iba1   gfap braak_stage
##    <chr>        <dbl> <fct>      <dbl>  <dbl>  <dbl>  <dbl> <fct>      
##  1 A1              81 AD        141017 230227  32959  26196 6          
##  2 A2              78 AD        141082 214944 204381  26739 6          
##  3 A3              80 AD         40788  46663      0  29308 2          
##  4 A4              85 AD         78770 136101  98074  41177 3          
##  5 A5              81 AD        110573  42893 140591  75334 5          
##  6 A6              79 AD        125934 199602 133705  91069 5          
##  7 A7              70 AD         32826  31016  34544  27905 1          
##  8 A8              76 AD         95281  92308 116275 143759 4          
##  9 A9              80 AD         55035 154453  62074 126360 2          
## 10 A10             94 AD         53040   9099  39297 137833 2          
## 11 C1              78 Control    35684      0  38523  59819 1          
## 12 C2              77 Control    62182  29663  73422  52276 3          
## 13 C3              73 Control    49062 106332      0  73822 2          
## 14 C4              70 Control    10123      0  13962  96704 0          
## 15 C5              74 Control     1530   2169   2002  83280 0          
## 16 C6              73 Control    25514  49980  25771  53798 1          
## 17 C7              81 Control    24367  48786  23961  17561 1          
## 18 C8              69 Control    43628  36442  19467  41970 2          
## 19 C9              78 Control    48923  64880  16367 110464 2          
## 20 C10             77 Control     9688   3818  12424  59021 0

For context, tau protein and amyloid beta peptides from the amyloid precursor protein aggregate into neurofibrillary tangles and A-beta plaques, respectively, the brains of people with AD. Generally, the amount of both of these pathologies is associated with more severe disease. Braak stage is a neuropathological assessment of the amount of pathology in a brain that is associated with the severity of disease, where 0 indicates absence of pathology and 6 with widespread involvement in multiple brain regions. Aggregation of tau is also a consequence of normal aging, so must accompany neurological symptoms such as dementia to indicate an AD diagnosis post mortem. Note we have control samples as well as AD.

Tauopathy: tau protein accumulates in the cell bodies of affected neurons - Wikipedia

The histology measures tau, abeta, iba1, and gfap have been quantified using digital microscopy, where brain sections are stained with immunohistochemistry to identify the location and degree of pathology; the measures in the table are the number of pixels of a 400 x 400 pixel image of a piece of brain tissue that fluoresce when stained with the corresponding antibody. Tau and A-beta antibodies are specialized to the types of aggregated proteins mentioned above and provide a quantification of the level of overall AD pathology. Ionized calcium binding adaptor molecule 1 (IBA1) is a marker of activated microglia, the resident macrophages of the brain, which is an indication of neuroinflammation. Glial fibrillary acidic protein (GFAP) is a marker for activated astrocytes, specialized cells that derive from the neuron lineage, are critical for maintaining the blood brain barrier, and are also involved in the neuroinflammatory response.

Let’s say we wished to visualize the relationship between age at death and the amount of tau pathology. A scatter plot where each marker is a subject with \(x\) and \(y\) position corresponding to age_at_death and tau respectively. The following R code creates such a plot with ggplot2:

ggplot(data=ad_metadata, mapping = aes(x = age_at_death, y=tau)) +
  geom_point()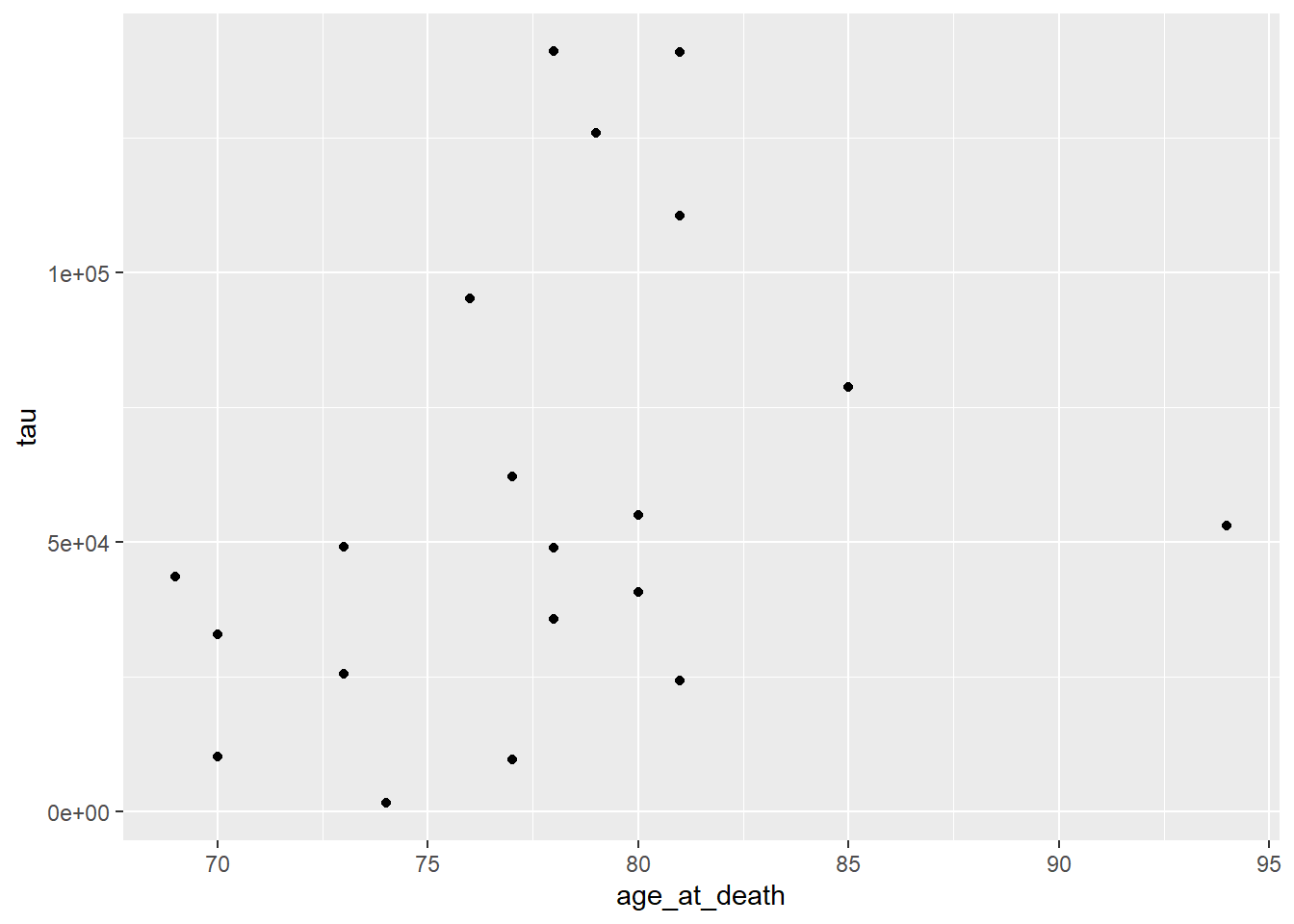

All ggplot2 plots begin with the ggplot() function call, which is passed a tibble with the data to be plotted. We then define the aesthetics are defined by mapping the x coordinate to the age_at_death column and the y coordinate to the tau column with aes(x = age_at_death, y=tau). Finally, the geometry as ‘point’ with geom_point(), meaning marks will be made at pairs of x,y coordinates. The plot shows what we expect given our knowledge of the relationship between age and amount of tau; the two look to be positively correlated.

However, we are not capturing the whole story: we know that there are both AD and Control subjects in this dataset. How does condition relate to this relationship we see? We can layer on an additional aesthetic of color to add this information to the plot:

ggplot(data=ad_metadata, mapping = aes(x = age_at_death, y=tau, color=condition)) +
  geom_point()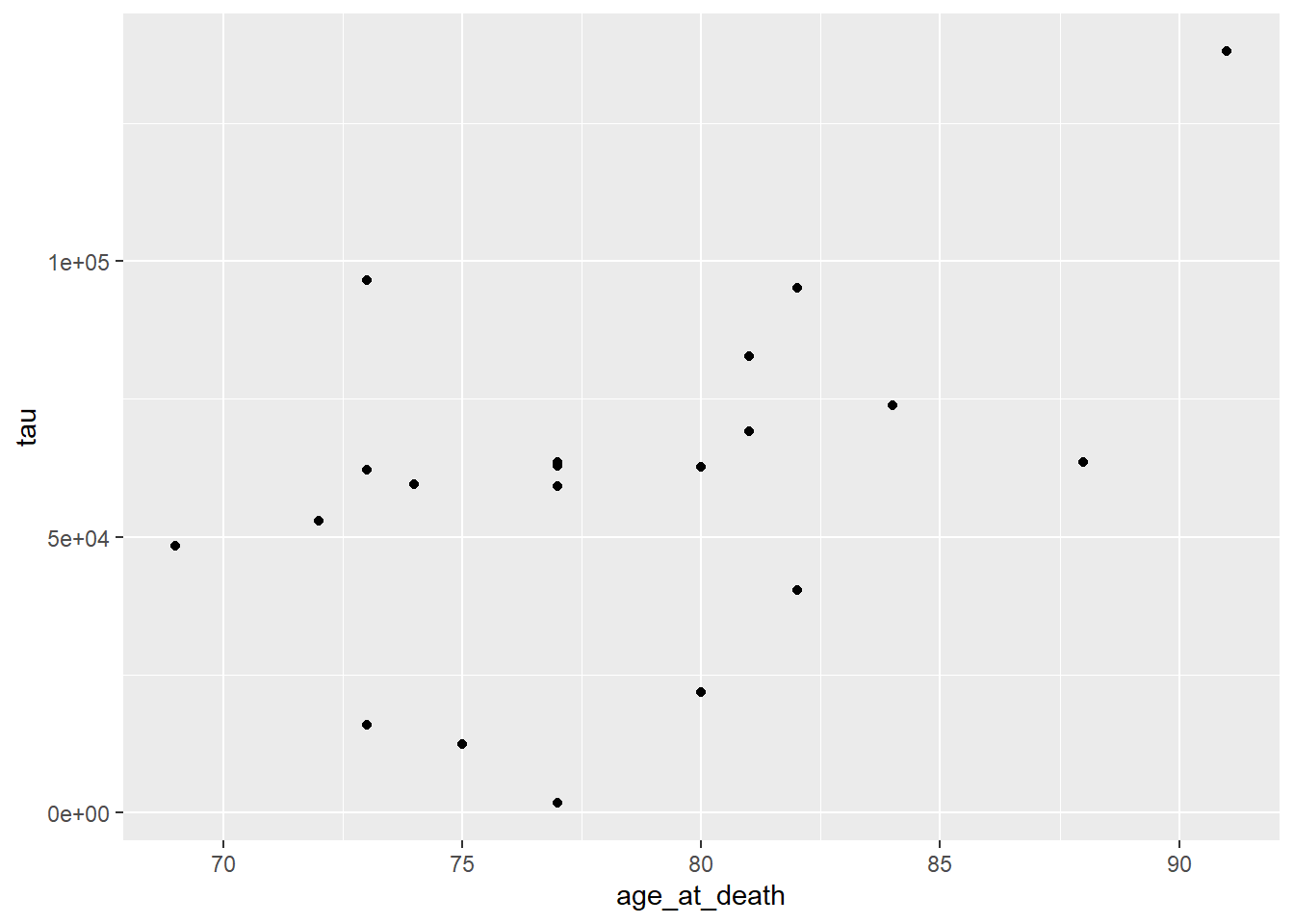

This looks a little clearer, showing that Control subjects generally have both an earlier age at death and a lower amount of tau pathology. This might be a problem, however, since if the age distributions of AD and Control groups are different that might pose a problem with confounding. We should investigate this.

Instead of plotting age at death and tau against each other, we will examine the distributions of each of these variables for AD and Control samples separately. We will use the violin geometry with geom_violin() to look at the distributions of age_at_death:

ggplot(data=ad_metadata, mapping = aes(x=condition, y=age_at_death)) +
  geom_violin()

We can see immediately that there are big differences between the age distributions of the two groups. This is not ideal, but perhaps we can adjust for these effects in downstream analyses. We’d like to look at the tau distributions as well, but it would be nice to have these two plots side by side in the same plot. To do that, we will use another library called patchwork, which allows independent ggplot2 plots to be arranged together with a simple expressive syntax:

library(patchwork)
age_boxplot <- ggplot(data=ad_metadata, mapping = aes(x=condition, y=age_at_death)) +
  geom_boxplot()
tau_boxplot <- ggplot(data=ad_metadata, mapping=aes(x=condition, y=tau)) +
  geom_boxplot()

age_boxplot | tau_boxplot # this puts the plots side by side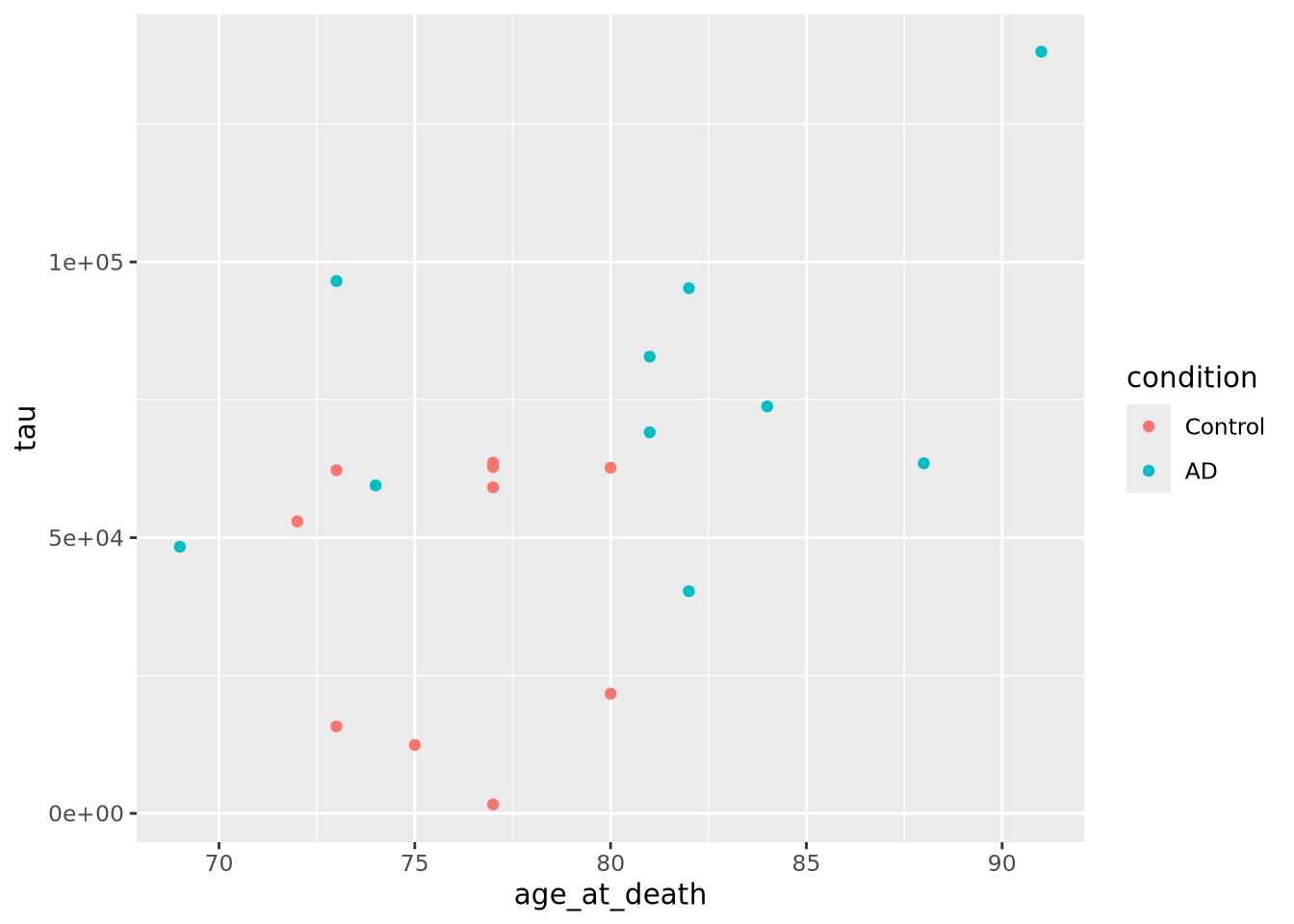

This confirms our suspicion, and also reveals a serious problem with our samples: we have strong confounding of tau and age at death between AD and Control samples. This means that if we look for differences between AD and Control, we won’t know if the difference is due to the amount of tau pathology or due to age of the subjects. With this sample set, we simply cannot confidently answer that question. Just a few simple plots alerted us to this problem; hopefully more expensive datasets have not already been generated for these samples, so that hopefully different subjects are available that could avoid this confounding.

This has been a biological data analysis oriented tutorial on plotting meant to illustrate the principles of the grammar of graphics. Namely, every plot has data, geometry, and aesthetics that can be independently controlled to produce many types of plots. Many of these plots have names, like scatter plots and boxplots, but as you compose different types of geometries and aesthetics together you may find yourself generating plots that aren’t so easily named.

The next sections of this chapter are a kind of “cook book” of different kinds plots you can generate with data of different shapes. It is not intended to be comprehensive, but a helpful guide when you are trying to decide how to visualize your own datasets.